Grundgesamtheit und Stichprobe: Unterschied zwischen den Versionen
(Seite wurde neu angelegt) |
Keine Bearbeitungszusammenfassung |
||
| (3 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 18: | Zeile 18: | ||
== Wie bekommt man eine Stichprobe? == | == Wie bekommt man eine Stichprobe? == | ||
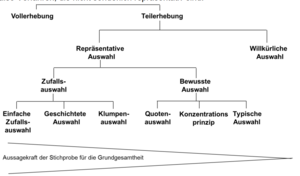
Grundsätzlich kann man verschiedene Arten des Stichprobenziehens voneinander unterscheiden (vgl. Abbildung). Von besonderer Bedeutung für Forschungszwecke ist die repräsentative Auswahl – und hierbei insbesondere die Zufallsverfahren. „Repräsentativität“ bezeichnet das Ausmaß, in dem eine Stichprobe die Struktur der Grundgesamtheit in bestimmter Hinsicht getreu widerspiegelt. In einzelnen Marktforschungsanwendungen werden Verfahren mit bewusster Auswahl eingesetzt, also Verfahren, die nicht sonderlich repräsentativ sind. | Grundsätzlich kann man verschiedene Arten des Stichprobenziehens voneinander unterscheiden (vgl. Abbildung). Von besonderer Bedeutung für Forschungszwecke ist die repräsentative Auswahl – und hierbei insbesondere die Zufallsverfahren. „Repräsentativität“ bezeichnet das Ausmaß, in dem eine Stichprobe die Struktur der Grundgesamtheit in bestimmter Hinsicht getreu widerspiegelt. In einzelnen Marktforschungsanwendungen werden Verfahren mit bewusster Auswahl eingesetzt, also Verfahren, die nicht sonderlich repräsentativ sind. | ||
Die Bandbreite von Stichprobengrößen liegt zwischen einigen und über 10.000 Befragungspersonen. Die Stichprobengröße hängt vor allem davon ab: | |||
* ob die Ergebnisse repräsentativ sein sollen oder ob eine bestimmte Fehlertoleranz nicht überschritten werden soll, | |||
* inwieweit die Ergebnisse in den jeweiligen Teilmengen noch repräsentativ sein sollen, | |||
* und wie groß die Grundgesamtheit ist. | |||
=== Beispiele === | |||
Folgende Tabelle zeigt Beispiele für verschieden große Stichproben auf: | |||
[[Datei:Stichprobenerhebung.png|mini|Abbildung: Stichprobenverfahren. Eigene Darstellung]] | |||
{| class="wikitable" | |||
|+ | |||
!Art der Befragung | |||
!befragte Personen | |||
|- | |||
| colspan="2" |'''Kleine Stichproben bis max. 100 Befragungen''' | |||
|- | |||
|Einzelgespräche, z.B. mit Expert*innen | |||
|5 - 10 | |||
|- | |||
|Kleine Grundgesamtheiten, z.B. Großchemie | |||
|ca. 5 | |||
|- | |||
|Produkttests | |||
|10 - 50 | |||
|- | |||
|Gruppendiskussionen | |||
|6 - 10 je Gruppe | |||
|- | |||
| colspan="2" |'''Mittlere und große Stichproben über 100 Befragungen''' | |||
|- | |||
|Auswahl aus Kunden- und Interessentendateien | |||
|bis 200 | |||
|- | |||
|Schriftliche Begragung | |||
|ab 200 | |||
|- | |||
|Bevölkerung | |||
|500 - 2.500 | |||
|- | |||
|Panelerhebungen bei Privatpersonen | |||
|ca. 10.000 | |||
|} | |||
<sup>Tabelle: Beispiele für die Festlegung von Stichprobengrößen<ref>Kastin 2008, S. 105 </ref>.</sup> | |||
Eine optimale Stichprobengröße gibt es also nicht. Sie ist bei jedem Untersuchungsgegenstand neu festzulegen. Nicht in jedem Fall macht es Sinn, die Stichprobengröße zu erhöhen, um genauere bzw. repräsentativere Ergebnisse zu erhalten. Aus Fehlertoleranztabellen ist zu entnehmen, dass die Verdoppelung einer Stichprobe von 2.000 auf 4.000 Befragungen die Genauigkeit lediglich um etwa einen Prozentpunkt verbessern würde. Ob sich der Mehraufwand (vor allem in finanzieller Hinsicht) einer größeren Stichprobe tatsächlich lohnt, muss gut überlegt sein. | |||
Da Stichproben aus Teilmengen der Grundgesamtheit bestehen, schwanken die Ergebnisse um den wahren Wert, der aus einer Vollerhebung resultieren würde, in einem bestimmten Fehlerbereich (vgl. hierzu auch den Abschnitt „Inferenzstatistik“). Dieser Abweichungsfehler hängt bei der zufallsgesteuerten Auswahl von der Stichprobengröße und dem Stichprobenwert ab. | |||
Die Größe der Stichprobe ist meist durch finanzielle Überlegungen determiniert. Ein wesentlicher Indikator zur Bestimmung der Größe der Stichprobe ist jedoch der Stichprobenfehler: Das heißt, wie exakt sind die Ergebnisse bzw. wie exakt sollen die Ergebnisse sein? (Nicht zu verwechseln mit der Repräsentativität!!!). Die anschließende Tabelle gibt Aufschluss über den Stichprobenfehler bei unterschiedlichen Stichprobenumfängen und Anteilen (ohne Endlichkeitskorrektur, nur für große Grundgesamtheiten). | |||
==Siehe auch== | |||
*[[Darstellung der Methode]] | |||
*[[Operationalisierung]] | |||
==Literatur== | |||
<references /> | |||
Aktuelle Version vom 12. März 2024, 15:08 Uhr
Hintergrund
Bei einer Vollerhebung würde man die interessierenden Personen/Gruppen komplett in eine Befragung einbeziehen. Dieses Vorgehen ist in der Praxis aber selten durchführbar. Zum einen ist es unwahrscheinlich, dass alle Personen einer Zielgruppe bereit sind, an einer Befragung teilzunehmen, zum anderen ist eine Vollerhebung zu zeit- und kostenintensiv[1][2]. Das Ziel einer wissenschaftlichen Erhebung ist es somit, Rückschlüsse aus einer kleineren Untersuchungsstichprobe auf eine größere Gesamtheit, die Grundgesamtheit, zu ziehen. Die erhobenen Daten werden in den seltensten Fällen dazu genutzt, nur über die Beobachteten, Befragten Aussagen zu treffen. Sie werden auf Personen, Gruppen usw. übertragen („generalisiert“), die nicht beobachtet, befragt oder analysiert worden sind.
Definitionen
Grundgesamtheit
Als Grundgesamtheit wird die gesamte Zielgruppe einer Erhebung, aus der eine Stichprobe von Versuchspersonen (Befragte) gezogen wird, bezeichnet. Die wichtigste Voraussetzung hierfür ist, dass die Grundgesamtheit bekannt ist oder anders formuliert: Die Grundgesamtheit muss empirisch definiert werden können. Hinter dieser Forderung steht eine ganz praktische Überlegung. Es ist nur möglich, von der Stichprobe auf die Grundgesamtheit zu schließen, wenn sichergestellt ist, dass die Stichprobe ein adäquates Abbild der Grundgesamtheit ist.
Stichprobe
Eine Stichprobe ist eine Auswahl von Elementen (n) aus einer Gesamtheit aller Elemente (N), die durch ein oder mehrere gleiche Merkmale gekennzeichnet sind. Der Umfang der Stichprobe bestimmt, mit welcher Genauigkeit und Zuverlässigkeit die Ergebnisse interpretiert und Aussagen über ihre Gültigkeit (über die Stichprobe hinausgehend) getroffen werden können.
Zufallsstichprobe
Eine Zufallsstichprobe ist ein Verfahren der Ziehung von Elementen aus einer Grundgesamtheit, für das folgende Kriterien gelten müssen: (1) Die Grundgesamtheit muss bekannt und exakt definiert sein; (2) Die Grundgesamtheit muss physisch oder symbolisch präsent und manipulierbar sein (sie muss sich durchmischen lassen, jedes Element muss entnehmbar sein); (3) Jedes Element darf nur einmal in der Grundgesamtheit vertreten sein; (4) Die Auswahl muss so erfolgen, dass jedes Element die gleiche oder eine berechenbare Auswahlchance (größer 0) hat, in die Stichprobe zu gelangen
Ziel einer wissenschaftlichen Studie muss es sein, Rückschlüsse von den Untersuchungsergebnissen der Stichprobe auf die Grundgesamtheit zu ziehen. Dafür werden jedoch an die Art und Größe der Stichprobe bestimme Anforderungen gestellt, damit die Stichprobe repräsentativ ist für die Grundgesamtheit: Die Art der Stichprobe sollte also ein Miniatur-Abbild der Grundgesamtheit sein. Um eine repräsentative Stichprobengröße zu erhalten, geht es nicht um die absolute Zahl von Untersuchungselementen, sondern um das zahlenmäßige Verhältnis von Grundgesamtheit und Stichprobe. Wichtig für den Aspekt der Repräsentativität ist zudem, dass es sich um eine zufällige Stichprobe handelt.
Wie bekommt man eine Stichprobe?
Grundsätzlich kann man verschiedene Arten des Stichprobenziehens voneinander unterscheiden (vgl. Abbildung). Von besonderer Bedeutung für Forschungszwecke ist die repräsentative Auswahl – und hierbei insbesondere die Zufallsverfahren. „Repräsentativität“ bezeichnet das Ausmaß, in dem eine Stichprobe die Struktur der Grundgesamtheit in bestimmter Hinsicht getreu widerspiegelt. In einzelnen Marktforschungsanwendungen werden Verfahren mit bewusster Auswahl eingesetzt, also Verfahren, die nicht sonderlich repräsentativ sind.
Die Bandbreite von Stichprobengrößen liegt zwischen einigen und über 10.000 Befragungspersonen. Die Stichprobengröße hängt vor allem davon ab:
- ob die Ergebnisse repräsentativ sein sollen oder ob eine bestimmte Fehlertoleranz nicht überschritten werden soll,
- inwieweit die Ergebnisse in den jeweiligen Teilmengen noch repräsentativ sein sollen,
- und wie groß die Grundgesamtheit ist.
Beispiele
Folgende Tabelle zeigt Beispiele für verschieden große Stichproben auf:
| Art der Befragung | befragte Personen |
|---|---|
| Kleine Stichproben bis max. 100 Befragungen | |
| Einzelgespräche, z.B. mit Expert*innen | 5 - 10 |
| Kleine Grundgesamtheiten, z.B. Großchemie | ca. 5 |
| Produkttests | 10 - 50 |
| Gruppendiskussionen | 6 - 10 je Gruppe |
| Mittlere und große Stichproben über 100 Befragungen | |
| Auswahl aus Kunden- und Interessentendateien | bis 200 |
| Schriftliche Begragung | ab 200 |
| Bevölkerung | 500 - 2.500 |
| Panelerhebungen bei Privatpersonen | ca. 10.000 |
Tabelle: Beispiele für die Festlegung von Stichprobengrößen[3].
Eine optimale Stichprobengröße gibt es also nicht. Sie ist bei jedem Untersuchungsgegenstand neu festzulegen. Nicht in jedem Fall macht es Sinn, die Stichprobengröße zu erhöhen, um genauere bzw. repräsentativere Ergebnisse zu erhalten. Aus Fehlertoleranztabellen ist zu entnehmen, dass die Verdoppelung einer Stichprobe von 2.000 auf 4.000 Befragungen die Genauigkeit lediglich um etwa einen Prozentpunkt verbessern würde. Ob sich der Mehraufwand (vor allem in finanzieller Hinsicht) einer größeren Stichprobe tatsächlich lohnt, muss gut überlegt sein.
Da Stichproben aus Teilmengen der Grundgesamtheit bestehen, schwanken die Ergebnisse um den wahren Wert, der aus einer Vollerhebung resultieren würde, in einem bestimmten Fehlerbereich (vgl. hierzu auch den Abschnitt „Inferenzstatistik“). Dieser Abweichungsfehler hängt bei der zufallsgesteuerten Auswahl von der Stichprobengröße und dem Stichprobenwert ab. Die Größe der Stichprobe ist meist durch finanzielle Überlegungen determiniert. Ein wesentlicher Indikator zur Bestimmung der Größe der Stichprobe ist jedoch der Stichprobenfehler: Das heißt, wie exakt sind die Ergebnisse bzw. wie exakt sollen die Ergebnisse sein? (Nicht zu verwechseln mit der Repräsentativität!!!). Die anschließende Tabelle gibt Aufschluss über den Stichprobenfehler bei unterschiedlichen Stichprobenumfängen und Anteilen (ohne Endlichkeitskorrektur, nur für große Grundgesamtheiten).
Siehe auch
Literatur
- ↑ Vgl. Kromrey, H: (2006). Empirische Sozialforschung: Modelle und Methoden der standardisierten Datenerhebung und Datenauswertung, 11. Aufl., Stuttgart: Lucius und Lucius, S. 279ff.
- ↑ Atteslander, P. (2008): Methoden der empirischen Sozialforschung, 12. Aufl., Berlin: Schmidt, S. 248ff.
- ↑ Kastin 2008, S. 105